Het moet iedereen opgevallen zijn: de coronacrisis heeft iets heel merkwaardigs laten zien met betrekking tot de wiskunde. Dag in dag uit worden we overstelpt met specifieke cijfers – aantal besmettingen, aantal ziekenhuisopnames, aantal patiënten op intensieve zorgen en aantal overlijdens – en met grafieken waar een specifieke woordenschat bij hoort zoals 'de exponentiële curve', 'de daling van de stijging', 'de piek' of 'het plateau'. In belangrijke mate worden al deze numerieke data bekomen via statistiek. De cijfers zijn de laatste tijd vervangen door weekgemiddelden – een niet zo eenvoudig concept, want het geeft aanleiding tot uitspraken zoals 'Het weekgemiddelde was 802 met een uitschieter gisteren van 1.075' – en de curves zijn ook op basis van die cijfers opgesteld. En dan heb ik het nog niet gehad over de besmettingsgraad – uitgedrukt door het fameuze 'reproductiegetal' – en de in procenten uitgedrukte efficiëntie van een vaccin. Wat betekent het juist dat een vaccin 90% effectief is?

MATHEMATICS IS HERE TO STAY!

Er kan al heel wat gezegd worden over de betrouwbaarheid van deze cijfers – in welke mate zijn bijvoorbeeld cijfers komende uit verschillende landen met elkaar vergelijkbaar? – en vooral hoe ze dienen geïnterpreteerd te worden. Maar dat is niet mijn onderwerp in deze bijdrage. Waar het mij om gaat is dat het hebben van deze cijfers cruciaal is om te begrijpen wat er aan de hand is. Het is op basis van deze wiskundige data dat wetenschappers, economen, zorgverleners en politici beslissingen hebben genomen. Dat klinkt weinig origineel. Want wat ik beweer is dat, als ik moet ingrijpen op een bepaalde situatie, het hebben van kennis en inzichten in die situatie mij vooruit kunnen helpen. Let wel, zo evident is dit nu ook weer niet. Want een teveel aan informatie kan verlammen. Dus moet je op zoek gaan naar methodes die veel informatie kunnen 'samenvatten' of 'comprimeren', en dat is precies wat statistiek doet. Ook hier is een 'let wel' van toepassing: dat samenvatten is zelden neutraal, zoals het klassieke voorbeeld van de intelligentiecoëfficiënt (IQ) heeft laten zien. Het complexe spel van verschillende vormen van intelligentie reduceren tot één enkele maat heeft belangrijke consequenties waarvan men zich bewust dient te zijn.

Los van deze kritische overwegingen, moge een ding evenwel duidelijk zijn: mathematics is here to stay! (om het eens sloganesk uit te drukken). En de vraag stelt zich spontaan: is corona het enige maatschappelijke probleem waar wiskunde zo'n belangrijke rol te spelen heeft? Of is haar rol algemener? Ik denk het tweede, en wel op basis van de gedachtegang dat (1) gegeven dat wiskunde op zoek gaat naar patronen en structuren zoals in de statistiek en (2) gegeven dat, zoals vermeld, inzichten helpen om verandering te plannen, het zo goed als onvermijdelijk is dat (3) wiskunde een rol te spelen heeft in het analyseren en begrijpen van en inspelen op maatschappelijke veranderingen.

Een specifieke instantie van zo'n veranderingsproces is een politieke beweging die zich wenst te heroriënteren in het maatschappelijke veld, geïnitieerd door een naamsverandering. Wat, is de vraag, kan wiskunde specifiek bijdragen aan Vooruit?

KENNIS EN KENNIS OVER KENNIS

Om te beginnen kan wiskunde op verschillende wijzen tussenkomen. Dat klinkt triviaal maar is het niet. Het is één ding om te begrijpen hoe bepaalde economische, sociale en politieke processen zich ontvouwen, het is een geheel ander ding om, op basis van die kennis en inzichten, te handelen en bepaalde doelen te realiseren. Maar het is nog een ander ding indien de vraag is hoe de groep zich dient te organiseren om tot die realisatie bij te dragen. In kernwoorden uitgedrukt, komen de drie mogelijkheden overeen met:

(a) Het hebben van kennis van de wereld,
(b) Het hebben van kennis over hoe de wereld te transformeren,
(c) Het hebben van kennis over hoe de kennis in (a) en (b) verzameld, samenhangt met de structuur van de groep die deze kennis heeft.

Ik zal niet ingaan op (a) en (b) omdat die al uitvoerig worden bestudeerd. Wat (a) betreft, hebben we het eigenlijk over zo goed als alle humane en sociale wetenschappen, en de rol die de wiskunde daarin speelt is bekend. Economen, psychologen, sociologen, politicologen … houden zich allen hiermee bezig. En wat (b) betreft, geldt hetzelfde. Wat doen decisie- en speltheorie anders dan processen bestuderen waarin mensen of groepen van mensen proberen te komen tot een keuze die aan vooraf gestelde voorwaarden voldoet? Maar (c) is, naar mijn inschatting, misschien wel al goed bestudeerd maar nog niet echt doorgedrongen buiten de wetenschappelijke wereld.

Ergens mag dat geen verbazing wekken. Want als we spreken over kennis, dan denken we in de eerste plaats aan een individu. Doe de oefening. Als ik zeg 'X weet dat het morgen zal regenen' en ik vraag wie of wat X kan zijn, dan zullen we toch geneigd zijn om voor X de naam van een individu in te vullen: 'Sabine Hagedoren weet dat het morgen zal regenen'. Maar zou het niet kunnen dat X een groep mensen is? Of een groep mensen tezamen met computers en/of andere instrumenten erbij? In de volgende sectie werk ik dit idee verder uit. Maar om te vermijden dat de lezer nu al afhaakt in de gedachte dat X als groep werkelijk nergens op slaat, dit eenvoudig voorbeeld. Stel dat drie mensen toegang hebben tot een kluis met een bepaalde code. Wat is interessanter? Dat iedereen de volledige code heeft of dat de code in drie wordt gedeeld en elk een stuk kent? In het eerste geval kunnen drie mensen de code verspreiden, in het tweede geval zo goed als zeker niemand. De sleutel is wel degelijk hoe de kennis, in dit geval van de code, verspreid is over deze groep van drie mensen. De algemene wetenschap die dit type problemen bestudeert staat bekend als netwerktheorie of netwerkwetenschap (network science).

EEN PAAR ELEMENTEN VAN NETWERKTHEORIE

Het is niet mijn bedoeling om diep in de wiskundige details te duiken en daarom gebruik ik een zo concreet mogelijk voorbeeld. Laat de groep X samengesteld zijn uit 100 mensen. Met x(i) bedoel ik niets anders dan de i-de persoon in de groep zodat de samenstelling van de groep als volgt kan worden voorgesteld: x(1), x(2), …, x(99), x(100). Als een persoon x(i) informatie kan doorgeven aan persoon x(j) dan is er een link van x(i) naar x(j) of, in half wiskundige notatie, x(i) --> x(j). Wat we verstaan onder de structuur van de groep X is een lijst van linken, anders gezegd, wie heeft met wie contact. En wat blijkt? Er zijn heel wat structuren denkbaar. Ik geef twee eenvoudige voorbeelden.

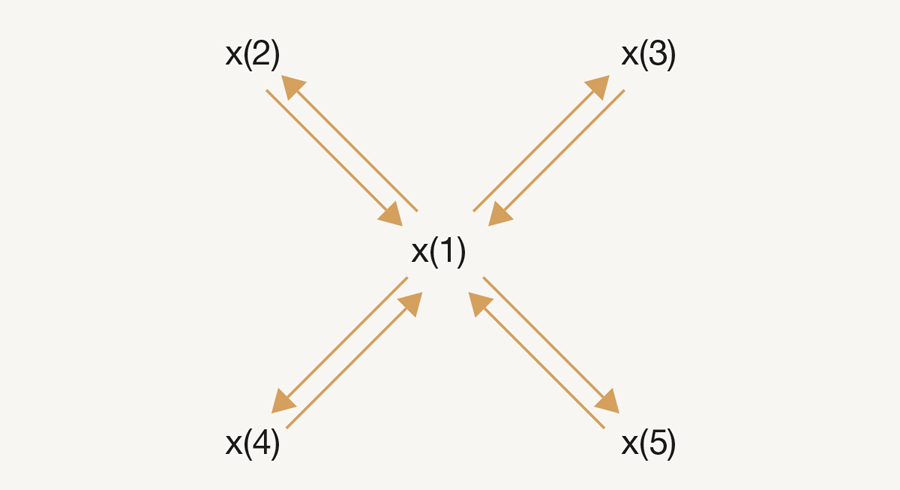
Voorbeeld 1. Er is één persoon, stel x(1) die de eigenschap heeft dat alle anderen een link hebben met x(1) en omgekeerd en onderling is er geen enkel contact. In half wiskundige notatie wordt dat: (1) voor alle i, verschillend van 1, hebben we x(1) --> x(i) en x(i) --> x(1), en (2) voor alle i en j, verschillend van 1, is er geen link tussen i en j. Grafisch krijg je een ster (AFBEELDING 1). In het midden zit x(1) die met iedereen kan communiceren maar niemand kan onderling met elkaar spreken. Dit is een goede benadering van een dictatuur. Iedereen is afhankelijk van één bron en beschikt niet over de mogelijkheid om met anderen te overleggen.

AFBEELDING 1: Een goede benadering van een dictatuur.

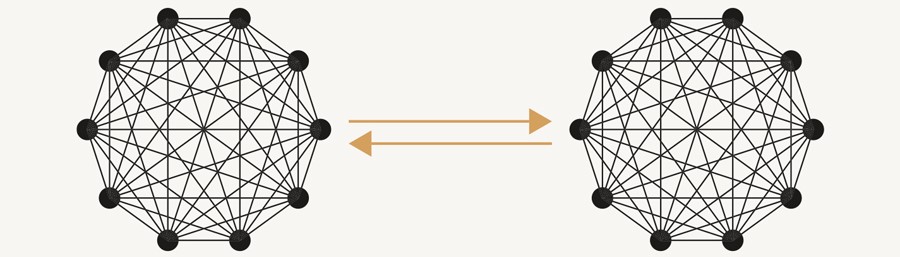
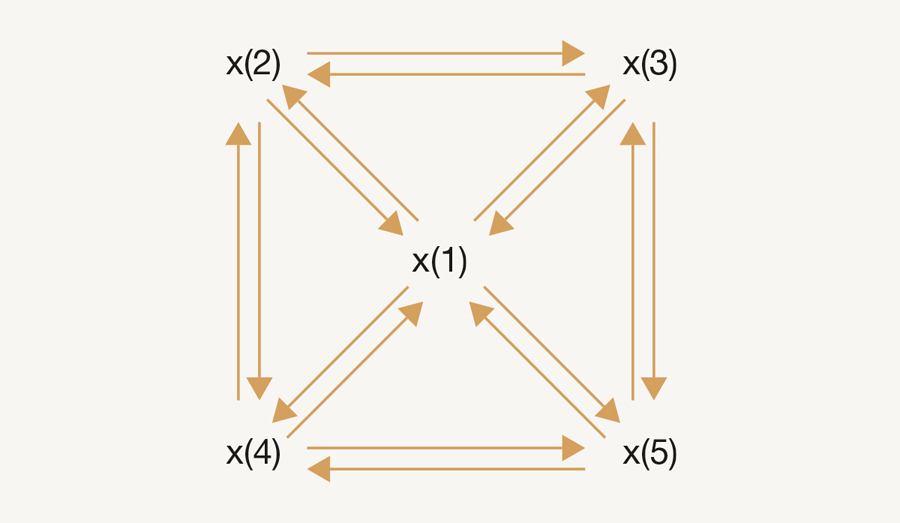
Voorbeeld 2. Iedereen heeft met iedereen contact dus, voor alle i en j, is er een link x(i) --> x(j). Grafisch levert dit een netwerk waar alle mogelijke pijlen kunnen getekend worden (AFBEELDING 2). Zouden we dit de perfecte democratie durven noemen? Misschien wel, maar efficiënt kan het moeilijk genoemd worden. Vertaal het even naar sociale media. Is het wenselijk dat mijn Twitterberichten door alle andere twitteraars gelezen worden? Erger nog, is het wenselijk dat ik alle berichten van anderen ontvang? Met een miljoen gebruikers is het aantal links in de orde van duizend miljard. Neen dus.

AFBEELDING 2: Een niet-efficiënte democratie.

Met deze twee voorbeelden heb ik uiteraard twee extremen willen illustreren. Daartussen ligt een gigantische ruimte om te exploreren. Een manier om een greep te krijgen op het onderwerp is door het introduceren van nieuwe begrippen. Een van de belangrijkste concepten is de afstand tussen twee mensen x(i) en x(j). Die is gelijk aan de kortste keten van linken tussen x(i) en x(j). Zo is de afstand voor twee willekeurige mensen in het eerste voorbeeld, behalve x(1), 2 omdat de kortste keten x(i) --> x(1) --> x(j) is. Voor x(1) is de afstand tot iedereen gelijk aan 1. Merk op dat de afstand onafhankelijk is van het aantal leden in de groep. In het tweede voorbeeld is de afstand voor iedereen 1 omdat iedereen met iedereen verbonden is. Wat zijn we hiermee? Gegeven een netwerk, kunnen we blijkbaar gemakkelijk de afstanden berekenen maar wat met de omgekeerde vraag? Stel dat je wil dat de afstand tussen twee mensen voldoende klein is, hoe moet je het netwerk organiseren? Dat blijkt geen gemakkelijke vraag te zijn en maakt een belangrijk onderdeel uit van netwerktheorie. Dit vraagt om een voorbeeld.

Voorbeeld 3. Stel dat de groep van 100 mensen uiteenvalt in 10 groepen van telkens 10 mensen. Neem aan dat binnen een groep van 10 iedereen met iedereen in contact kan zijn dus is de afstand in zo'n deelgroep 1. Stel nu dat in een groep één lid een link heeft met één lid uit een andere groep. Dan is de afstand tussen een lid van de ene en een lid van de andere groep maximum 3 want je kan de volgende keten maken: x(i) in groep 1 --> contactpersoon met groep 2 --> contactpersoon met groep 1 --> x(j) in groep 2. Dit betekent dat voor de twee groepen samen de afstand maximum 3 is (AFBEELDING 3).

AFBEELDING 3: Een goed geconnecteerd netwerk.

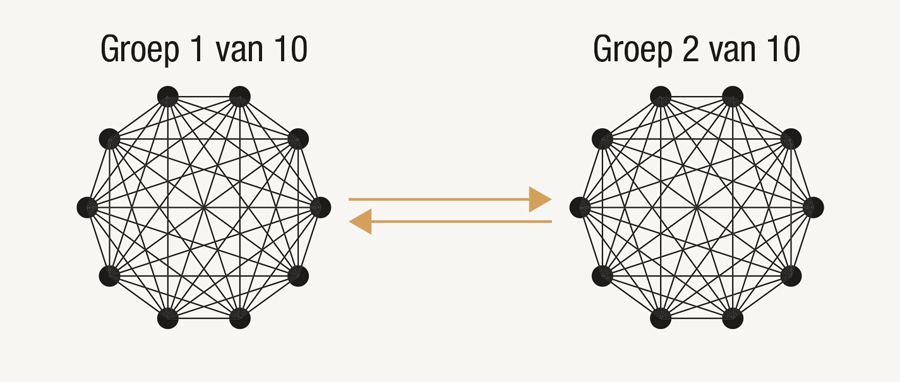
Wat hieruit te leren valt, is dat één link voldoende kan zijn om twee groepen met elkaar in contact te brengen zonder dat de afstand dramatisch stijgt. Wat hier wordt aangetoond is, om het in mensentaal uit te drukken, het belang van 'go-betweens'. Wat leidt tot een belangrijk inzicht: een individu kan van enorm belang zijn in een groep indien hij of zij op het juiste moment de juiste plaats in een netwerk inneemt. Wat meteen ook verklaart waarom sommige individuele inspanningen tot iets leiden en andere niet. Een misschien nog belangrijker inzicht – en dan laat de wiskunde zich van haar mooiste kant zien – is dat voorbeeld 3 laat zien dat, om een goed geconnecteerd netwerk te bekomen, het allerminst vereist is dat er een hiërarchische structuur moet worden geïnstalleerd. Bedenk ten slotte dat ik nu nog met geen woord heb gesproken over de dynamiek van dergelijke netwerken en het is duidelijk dat netwerktheorie een omvangrijk en fascinerend onderzoeksgebied is.

BESLUIT

Vermoedelijk heeft een aantal lezers bij voorbeeld 3 gedacht aan het curieuze fenomeen van de zogenaamde 'six degrees of separation', de bewering dat de gemiddelde afstand, zoals hierboven gedefinieerd, tussen twee mensen op aarde gelijk is aan 6. Er is op het ogenblik bewijsmateriaal voor en tegen, maar netwerktheorie maakt het mogelijk om de kwestie mathematisch aan te pakken. Dus stelt iemand de vraag hoe we ons zo kunnen organiseren dat iedereen meespeelt en toch de groep voldoende efficiënt kan handelen, zoals wellicht de beweging Vooruit zal beogen, verlies dan niet uit het oog dat de wiskunde een ruimte van mogelijkheden aanbiedt die, meen ik te mogen stellen, onvoldoende wordt geëxploreerd.

VOETNOOT

Laat het duidelijk zijn dat de studie van concrete, specifieke netwerken al zeer oud is. Een neuroloog kijkt naar neurale netwerken, een computerwetenschapper naar digitale netwerken, een organisatiesocioloog naar sociale netwerken, een bioloog naar symbiotische netwerken… In deze tekst heb ik het over de wiskundige studie van netwerken, los van mogelijke toepassingen. Ook in die zin maakt het deel uit van een ouder wiskundig domein, namelijk de zogenaamde grafentheorie. Maar het samenbrengen van de concrete en de mathematische netwerken is iets van recentere oorsprong en één van de eerste sleutelwerken in dit verband is het boek van Duncan J. Watts, 'Small Worlds. The Dynamics of Networks between Order and Randomness' (Princeton: Princeton University Press, 1999).

Samenleving & Politiek, Jaargang 27, 2020, nr. 10 (december), pagina 31 tot 35

• Vooruit
• sp.a
• beweging
• wiskunde

WAARHEEN GAAT VOORUIT?

Is een ledenpartij passé?

Bram Wauters

Welk pad kiest Vooruit?

Wim Vermeersch

Nothing Left?

Matthias Somers

Vintage Vooruit

Geert Van Goethem

De democratische delta

Marian Cramers

Vooruit met de wiskunde

Jean Paul Van Bendegem